Warum das wichtig ist: Quantencomputer werden bereits in absehbarer Zeit die Forschung revolutionieren und in den Alltag Einzug halten. Je näher ihre kommerzielle Nutzung rückt, desto wichtiger wird auch die Ausbildung zukünftiger Fachkräfte. Da es so manches Missverständnis um Quantencomputer und deren Nutzungsweise gibt, sollten nicht nur Expert:innen wissen, wie sie funktionieren und wofür wir sie einsetzen könnten.
Eine technische Revolution, die die Welt verändern und unsere Computer irgendwann mal ablösen wird – so werden Quantencomputer oft wahrgenommen. Tatsächlich sind Quantencomputer aber keine Zukunftsmusik, es gibt schon heute funktionierende Anlagen. IBM Quantum System One ist Europas erster kommerziell nutzbarer Quantencomputer, der vor Kurzem im deutschen Ehningen, in der Nähe von Stuttgart, präsentiert wurde. Weitere Standorte in Europa befinden sich bereits in Planung, womit die Nutzung von Quantencomputern einen Schritt weiter in Richtung Alltag rückt. Das Exemplar in Ehningen ist mit einem Prozessor ausgestattet, der mit 27 Qubits arbeitet. Doch was sind Qubits eigentlich?
0, 1 und irgendwie beides
Qubits (quantum bits) sind die quantenphysikalische Version des Bits, mit dem der herkömmliche, klassische Computer arbeitet: Ein Bit kann den Wert 0 oder 1 speichern, und die gesamte Informationsverarbeitung verläuft in einer Abfolge dieser beiden Werte.
Ein Qubit kann mehr als das: Der Zustand |Ψ⟩ eines Qubits kann durch eine Superposition von zwei Zuständen |Ψ⟩= α|0⟩ + β|1⟩ beschrieben werden, wobei α und β komplexe Zahlen sind und als Gewichtungen der beiden Zustände |0⟩ und |1⟩ verstanden werden können. Diese Überlagerung wird manchmal als gleichzeitiges Vorhandensein der beiden einzelnen Zustände interpretiert.
Grafisch lassen sich Qubits z.B. mithilfe der Blochkugel veranschaulichen, in der ein Zustand in Form eines Pfeils in einer Kugel dargestellt wird. Die klassischen Bitwerte 0 und 1 befinden sich dabei an Nord- und Südpol, eine Superposition der beiden Zustände wird durch einen Pfeil in eine beliebige andere Richtung dargestellt, wobei die Zahlen α und β dessen Orientierung bestimmen (Audretsch, 2005).
Die Schreibweise |Ψ⟩ für physikalische Zustände geht auf den britischen Physiker Paul Dirac zurück. Bei diesen Objekten handelt es sich um Zustandsvektoren. Man kann sie als Spaltenvektoren auffassen, die die Information über das System enthalten. Anderswo werden Vektoren mit einem Pfeil über der Variable gekennzeichnet, diese Notation hat sich aber aus Gründen der besseren Übersicht bei Berechnungen nicht bewährt.
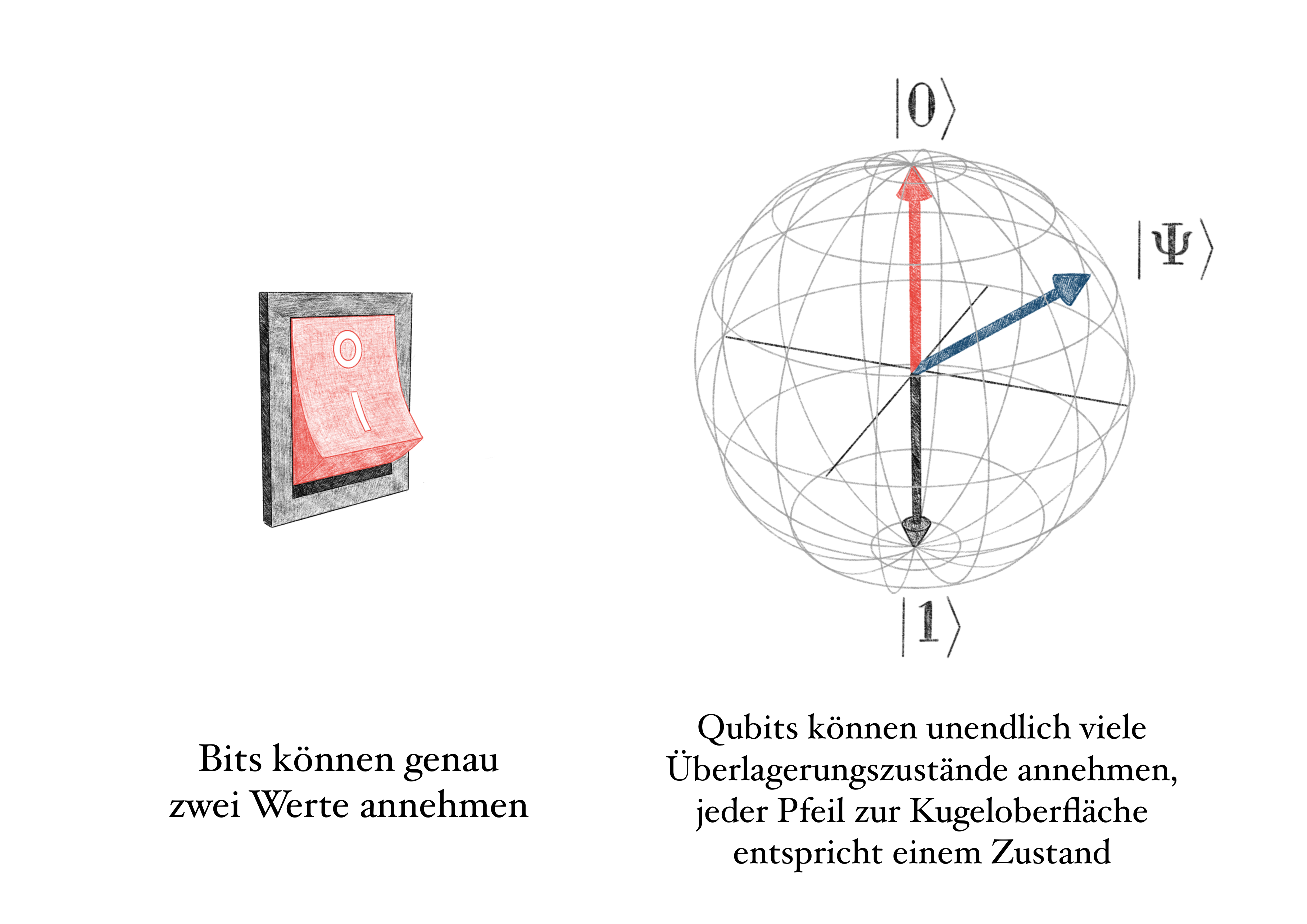
Abbildung 1: Ein klassisches Bit kann die Werte 0 und 1 besitzen, der Zustand eines Qubits bietet durch Superposition mehr Spielraum und kann mithilfe einer Blochkugel dargestellt werden. (Quelle: alamy.com / Autor)
So wie Bits auf unterschiedliche Weisen im Computer realisiert werden können (hohe/niedrige Spannungen, geladene/ungeladene Speicherelemente), dient auch das Qubit zunächst als Verallgemeinerung verschiedener physikalischer Systeme.
Ein konkretes Beispiel für ein Qubit ist die Beschreibung des Spins eines Teilchens. Subatomare Partikel wie Neutronen haben die Eigenschaft, in einem inhomogenen Magnetfeld von ihrer geradlinigen Bahn abgelenkt zu werden. Damit verhalten sie sich, als wären sie selbst kleine Magneten. Der gedachte Pfeil von Nord- zu Südpol wird mit dem Spin beschrieben. Die Orientierung des Spins wirkt sich dann auf die Richtung und Intensität der Ablenkung im Magnetfeld aus. Mit einem Detektorschirm, der die Auftreffpunkte nach Durchqueren des Magnetfelds festhält, kann also eine Messung des Spins stattfinden. Klassisch könnte der Spin in jede beliebige Raumrichtung zeigen, wodurch die Teilchen dann verschieden stark abgelenkt würden. Nachdem der Strahl den Magneten passiert hat, müsste er sich also kontinuierlich verbreitern.
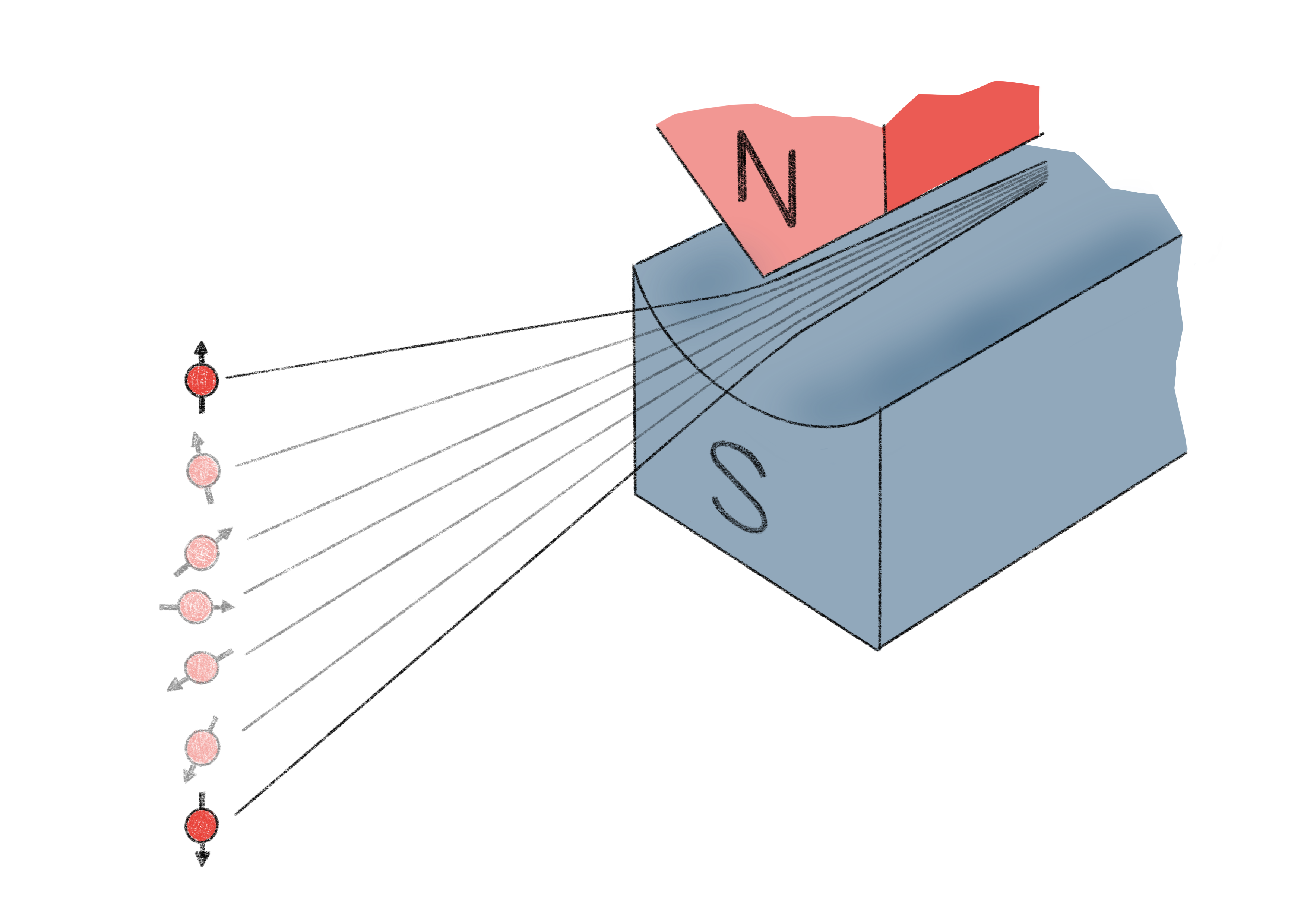
Abbildung 2: Klassische Erwartung bei einer Spin-Messung mit inhomogenem Magnetfeld und tatsächliches Resultat (hervorgehoben). (Quelle: godel-universe.com)
Entgegen dieser klassischen Erwartung lässt die Spin-Messung aber nur zwei Ergebnisse zu! Damit gibt es eine Quantisierung: Der Spin kann nur in zwei entgegengesetzte Richtungen zeigen, die wir mit den Werten „0“ und „1“ versehen. Vor der Messung liegt allerdings eine Superposition der beiden Zustände vor. Physikalische Systeme dieser Art, die bei Messungen nur zwei Ergebnisse zulassen, werden Zwei-Level-Systeme genannt und eignen sich als Qubits. (Nielsen & Chuang, 2010).
Wird an einem Qubit eine Messung durchgeführt, befindet es sich danach nicht mehr in Superposition. Ob nun |0⟩ oder |1⟩ gemessen wird, ist im Allgemeinen zufällig. Möchte man aber wissen, welches Ergebnis wahrscheinlicher ist, lohnt sich ein Blick auf die Blochkugel: Da prinzipiell jeder Punkt an ihrer Oberfläche durch einen Pfeil angesteuert werden kann, gibt es unendlich viele mögliche Superpositionen. Ist der Pfeil aber näher am 0-Pol, wird bei einer Messung mit größerer Wahrscheinlichkeit dieses Ergebnis festgestellt. Zeigt der Pfeil zum Äquator, sind beide Messergebnisse gleich wahrscheinlich (Audretsch, 2005).
Bei Qubits lassen sich also wie bei Bits nur zwei Werte messen. Wozu soll man sich also mit Superposition beschäftigen?
Alles auf einmal
Für die Ausführung von Algorithmen mit einem Quantencomputer werden üblicherweise mehrere Qubits betrachtet. Wird mit der Zustandsbeschreibung von zwei Qubits begonnen, können diese als Superposition der Zustände |00⟩, |01⟩, |10⟩ und |11⟩ gedeutet werden (wobei der erste Eintrag für das eine Qubit, der zweite für das andere steht), denn all diese Kombinationen könnten durch Messungen festgestellt werden. Während ein Qubit zwei überlagerte Zustände beinhaltet, kommen bei zwei Qubits bereits 2²=4 Zustände gleichzeitig vor, bei drei Qubits 2³=8 etc. Mit jedem weiteren Qubit verdoppelt sich also die Anzahl der sich überlagernden Zustände (Audretsch, 2005).
Vergleicht man die Arbeitsweisen von klassischen und Quantencomputern, wird ein wichtiger Unterschied deutlich: Führt ein klassischer Computer etwa eine Suche in einer Datenbank durch, wird sukzessive jeder einzelne Eintrag gefragt, ob er der Gesuchte ist. Erst im Falle eines Fundes wird der Algorithmus abgebrochen. In großen Datenbanken kann es dabei zu entsprechenden Wartezeiten kommen. Superposition erlaubt, sämtliche Eingabewerte durch einen Algorithmus parallel zu bearbeiten, da alle Eingaben gewissermaßen gleichzeitig vorliegen können (Homeister, 2018). Damit soll aber nicht der Eindruck entstehen, dass ein einmaliges Überprüfen reicht: Solche Algorithmen müssen zur Steigerung der Aussagekraft durchaus mehrfach durchgeführt werden. Trotzdem lässt sich vorhersagen, dass ein solcher Quantenalgorithmus effektiver als der beste klassische Algorithmus ist.
Das Superpositionsprinzip ist der erste bedeutende Unterschied zum klassischen Computer und einer der Gründe, warum Quantencomputer manche Aufgaben schneller lösen könnten.
Spukhafte Fernwirkung
Ein weiteres wichtiges Prinzip stellt der von Erwin Schrödinger geprägte Begriff der Verschränkung dar (Schrödinger, 1935). Darunter wird das Verhalten von mehreren Systemen verstanden, wenn diese nicht unabhängig voneinander beschrieben werden können. Misst man zwei verschränkte Qubits jeweils einzeln auf gleiche Art, kann bei beiden wiederum nur 0 oder 1 festgestellt werden. Ihre Verschränkung kann sich z.B. darin ausdrücken, dass nur gegengleiche Werte festgestellt werden, also 0 bei einem Qubit und 1 beim anderen oder umgekehrt. Andere Arten von Verschränkung lassen nur gleiche Messergebnisse zu. Allgemeiner gilt: Auch wenn man beide Systeme räumlich voneinander trennt und Messungen durchführt, zeigt sich bei verschränkten Systemen stets ein wohlbestimmter Zusammenhang der Messergebnisse, für Einstein eine „spukhafte Fernwirkung“. Die beiden Teilsysteme sind also voneinander abhängig und ihr Zustand ist nur zusammen korrekt zu beschreiben (Homeister, 2018).
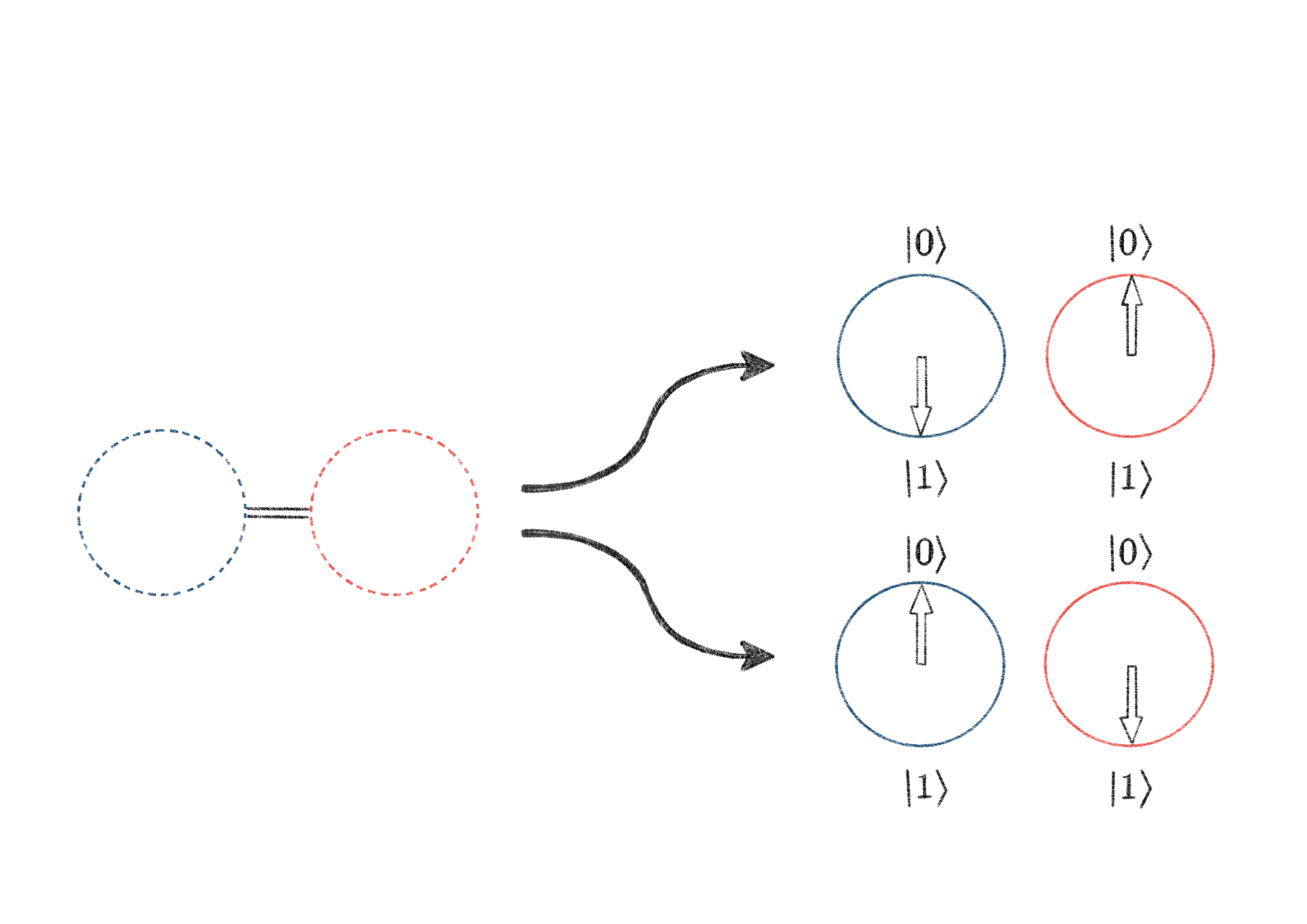
Abbildung 3: Bei manchen verschränkten Zuständen treten bei gleicher Art der Messung nur gegengleiche Messergebnisse auf, unabhängig von räumlicher Distanz. (Quelle: Autor)
Ein Beispiel für die Erzeugung verschränkter Systeme stellen Photonen dar: Photonen eignen sich als Qubits, da sie nach geeigneter Messung horizontal oder vertikal polarisiert sind – also wieder genau zwei Zustände oder deren Superposition annehmen können. Beim Durchqueren eines Kristalls kann ein Photon in zwei Photonen mit halbierter Energie übergehen. Anschließende Polarisationsmessungen ergeben stets gegengleiche Messergebnisse (Homeister, 2018).
Verschränkung spielt für viele Quantenalgorithmen eine große Rolle und ist in manchen Fällen der Grund, warum bestimmte Aufgaben schneller gelöst werden könnten. Konkret könnte dies etwa ermöglichen, RSA-Verschlüsselungen zu knacken, die z.B. im Telebanking benutzt werden. Auch zur abhörsicheren Kommunikation lässt sich Verschränkung nutzen (Ekert, 1991).
Eine Frage der Hardware
Der Spin eines Teilchens dient zwar als einigermaßen anschauliches Beispiel für die Superposition zweier Zustände, ist aber für die Realisierung eines Quantencomputers kein praxisrelevantes Beispiel. Photonen erweisen sich als geeigneter und wurden etwa zuletzt von Forscher:innen an der University of Science and Technology of China zur Realisierung eines Quantencomputers verwendet (Zhong et al., 2020).
Für die meisten Realisierungen von Qubits in Form eines Prozessors werden supraleitende Ringleiter verwendet. Hier gibt es verschiedene Möglichkeiten für Zwei-Level-Systeme, etwa das sogenannte Flux-Qubit (fließt Strom in die eine oder andere Richtung), oder das Charge-Qubit (findet man elektrische Ladungen in einem bestimmten isolierten Bereich im Ringleiter oder nicht) (Clarke et al., 2008). Solche Ausführungen lassen sich dann zweidimensional auf einer Platine anordnen. Eine Abwandlung des Charge-Qubits benutzten beispielsweise Forscher:innen, um Googles Sycamore-Prozessor herzustellen. Eigenen Aussagen zufolge gelang es mit diesem 2019 erstmals Quantenüberlegenheit zu demonstrieren: Die Forscher:innen konnten ein Problem mit einem Quantencomputer lösen, das kein klassischer Computer in akzeptabler Zeit bewältigen könnte (Arute et al., 2019).
In beiden Fällen handelt es sich um räumlich sehr kompakte Prozessoren – dennoch sind Quantencomputer vergleichsweise große Anlangen. Der aufwendige Aufbau dient dazu, das System möglichst von der Umwelt zu isolieren und auf äußerst tiefe Temperaturen zu kühlen. So möchte man Dekohärenz vermeiden: Durch Wechselwirkungen mit der Umwelt wird die Superposition zerstört, die Umgebung „misst“ sozusagen das System. Dies ist mitunter der Grund dafür, warum makroskopische Objekte im Alltag nie in Superposition vorliegen können. Da Superposition aber eine Voraussetzung für Quantencomputer ist, sollten Umgebungseinflüsse möglichst reduziert werden. Völlig verhindern lässt sich Dekohärenz nicht, sie muss aber auch nur für die Dauer eines Algorithmus hinausgezögert werden (Homeister, 2018).
Prepare, Measure, Manipulate, Repeat
Unabhängig von der tatsächlichen Realisierung funktioniert ein Quantenalgorithmus folgendermaßen: Zu Beginn werden alle Qubits in einem Zustand (z.B. |0⟩) präpariert. Die Ausführung des Algorithmus geschieht dann durch Manipulationen der Systeme, die den Zustand einzelner Qubits verändern oder z.B. zwei Qubits gekoppelt beeinflussen. Stellt man sich die Qubits abermals durch einen Pfeil in einer Blochkugel vor, entsprechen diese Manipulationen einer Veränderung der Pfeile darin (Homeister, 2018). Photonen werden beispielsweise durch eine Anordnung von Spiegeln, Strahlteilern und anderen optischen Hilfsmitteln geschickt, supraleitende Ringleiter werden mit regulierbaren Spannungen und externen Magnetfeldern auf gezielte Weise beeinflusst (Nielsen & Chuang, 2010).
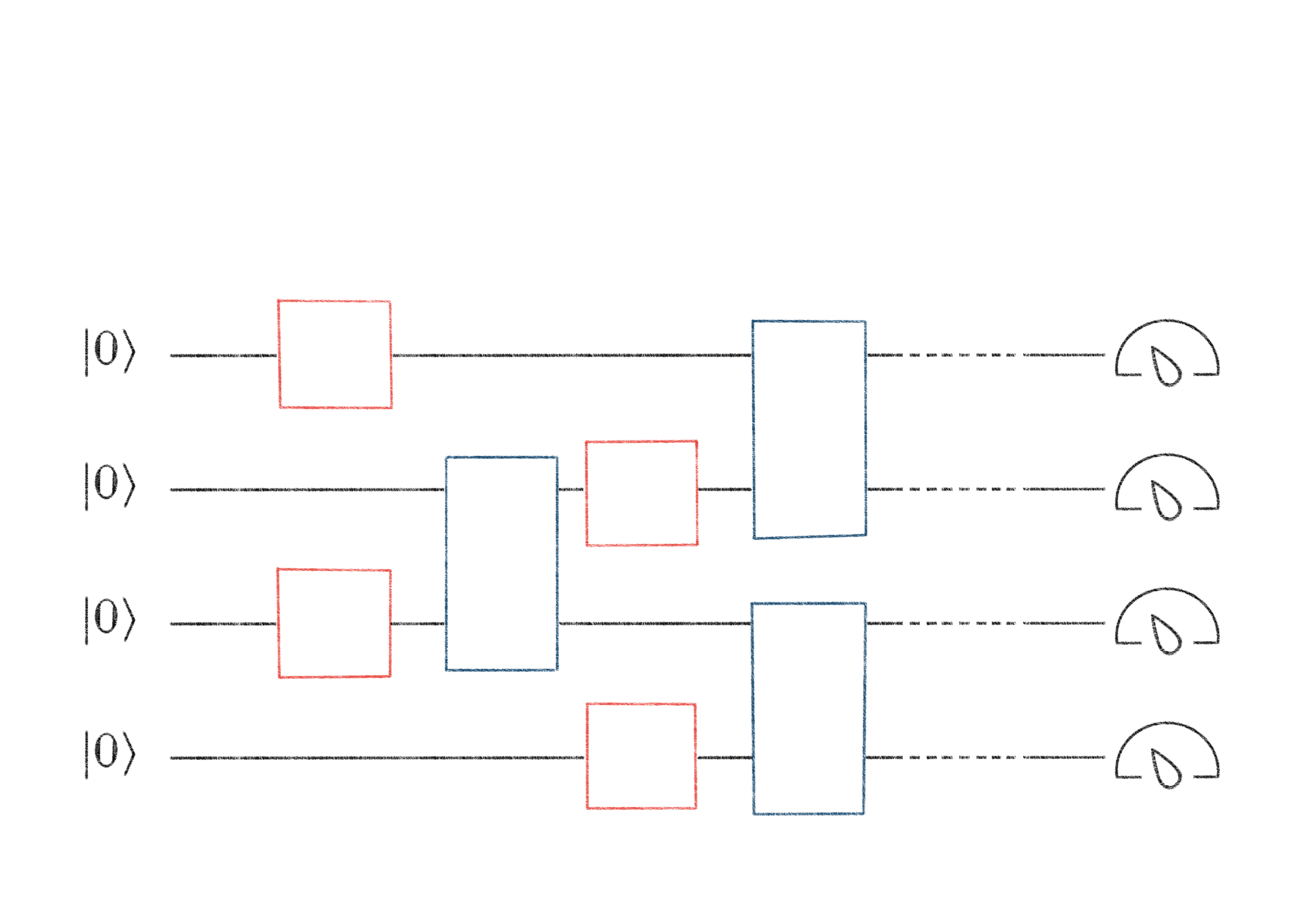
Abbildung 4: Schema eines Quantenschaltkreises mit Präparation, Manipulationen und abschließender Messung. (Quelle: Autor)
Beendet wird ein Algorithmus, indem eine Messung ausgeführt wird. Ist zum Beispiel die Position eines Elements in einer Datenbank gesucht, von dem wir ausnahmsweise schon wissen, dass es in der Liste an der Position 9 (oder binär 1001) steht, hat der Algorithmus die Aufgabe, die Pfeile in der Blochkugel so zu manipulieren, dass am Ende mit sehr hoher Wahrscheinlichkeit die Position des gesuchten Elements (hier 1001) gemessen wird. Da der Zufall eine wichtige Rolle bei Messungen spielt, kann es nach einmaligem Durchführen auch zu einem anderen Ergebnis kommen. Erst nach mehrmaliger Anwendung des Algorithmus und Häufung des Messergebnisses 1001 kann auf die Position 9 geschlossen werden.
Im Gegensatz zu Bits lassen sich Qubits nicht löschen oder kopieren. Auch die Behandlung von Fehlern unterscheidet sich: Bits lassen sich im klassischen Computer zwischenzeitlich messen und gegebenenfalls korrigieren, dies kann durch den nachhaltigen Einfluss einer Messung am Qubit aber nicht erfolgen. Allerdings lassen sich durch geschickte Konstruktion prinzipiell all diese Hindernisse umgehen, und tatsächlich lässt sich sogar jede Aufgabe, die von einem klassischen Computer bewältigt werden kann, theoretisch auch mit einem Quantencomputer bewerkstelligen (Homeister, 2018). Aber ist das ein wünschenswertes Zukunftsmodell?
Quantencomputer für alle?
Während manche Forscher:innen auf lange Sicht die Entwicklung eines Quantencomputers anstreben, der mit jeder berechenbaren Aufgabe betraut werden kann, wird von anderen zunächst nur die Lösung eines bestimmten mathematischen Problems angepeilt. Quantencomputern alle Aufgaben eines klassischen Computers zu übertragen wäre aufgrund des technischen Aufwands äußerst ineffizient. Vielmehr könnten sie sich dafür eignen, ganz bestimmte Aufgaben schneller zu bewältigen. Die Suche in einer Datenbank mittels des Grover-Algorithmus (Grover, 1996) und das Knacken der RSA-Verschlüsselung mithilfe des Shor-Algorithmus (Shor, 1994) sind Beispiele hierfür. Wegen den technischen Herausforderungen können diese aber noch nicht nutzbringend umgesetzt werden. Insofern sind für kommerzielle Anwendungen Hybridlösungen aus Quanten- und klassischen Computern denkbar, vollständig abgelöst soll letzterer also in Zukunft nicht werden (Homeister, 2018).
Mögliche Anwendungsfelder für Quantencomputer gibt es theoretisch zur Genüge: Sie könnten zu Fortschritten in Materialwissenschaften und Chemie beitragen, zudem gilt für aufwendige Machine Learning-Aufgaben das Feld des Quantum Machine Learning als aussichtsreicher Forschungsbereich. Damit könnten viele verschiedene Fachgebiete von weiterer Forschung profitieren, und Europas erster Quantencomputer könnte ein bedeutender Schritt in Richtung einer zukunftsweisenden Technologie sein.
David Schaubmair ist Lehrer für Mathematik und Physik. Im Rahmen seiner Masterarbeit in der Quantumparticlegroup unter der Leitung von Beatrix C. Hiesmayr beschäftigte er sich unter anderem mit Quantencomputer und wie diese im Schulunterricht thematisiert werden können. Sein Interesse gilt insbesondere Deutungsschwierigkeiten und Missverständnissen über die Quantenphysik, welche auch vermehrt in pseudowissenschaftlichem Rahmen anzutreffen sind.
- Superposition und Messung: Zur Ergründung dieser Konzepte gibt es einen kostenlosen und interaktiven Brilliant-Kurs.
- In diesem YouTube-Video werden diese Inhalte erneut anhand des Spin thematisiert und das Phänomen der Verschränkung damit anschaulich dargestellt. Dabei wird auch auf den Nachweis von Verschränkung eingegangen. (Veritasium)
- Eine mathematische Erklärung der RSA-Verschlüsselung mit Beispiel ist hier zu finden. (studyflix)
- Diese Anwendung erlaubt es, sich mit Quanten-Algorithmen vertraut zu machen und sie sogar auf echten Quantencomputern auszuprobieren. (IBM)
Schrödinger, E. (1935). Die gegenwärtige Situation in der Quantenmechanik. Naturwissenschaften 23, 844–849.
Ekert, A. K. (1991). Quantum cryptography based on Bell’s theorem. Physical Review Letters 67, 661–663.
Zhong, H.-S. et al. (2020). Quantum computational advantage using photons. Science (American Association for the Advancement of
Science), 1460–1463.
Arute, F. &, et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature, 505–510.
Clarke, J., Wilhelm, F. (2008). Superconducting quantum bits. Nature 453, 1031–1042.
Grover, L. J. (1996). A Fast Quantum Mechanical Algorithm for Database Search. Annual ACM Symposium on Theory of Computing,
212–219.
Shor, P. W. (1994). Algorithms for quantum computation: discrete logarithms and factoring. Proceedings 35th Annual Symposium on
Foundations of Computer Science, 124–134.
Audretsch, J. (2005). Verschränkte Systeme: die Quantenphysik auf neuen Wegen. Wiley-VCH.
Homeister, M. (2018). Quantum Computing verstehen: Grundlagen - Anwendungen - Perspektiven. Springer Vieweg.
Nielsen, M. A. &, Chuang, A. L. (2010). Quantum Computation and Quantum Information. Cambridge University Press.

.jpg)