Was kommt nach unendlich?

Warum das wichtig ist: Sie fasziniert uns, obwohl wir sie kaum begreifen können: die Unendlichkeit. Mathematiker:innen begegnet dieses Konzept häufig, doch was meinen wir eigentlich, wenn wir sagen, dass etwas unendlich groß ist? Wie viele verschiedene Unendlichkeiten gibt es und wie sehen diese aus? Und was kommt nach unendlich? Die mathematische Logik, genauer gesagt ihr Teilgebiet, die Mengenlehre, beschäftigt sich mit dem Begriff der Unendlichkeit und liefert präzise Antworten auf die oben genannten Fragen. Damit bildet sie die Grundlage für viele andere Gebiete in der Mathematik.

Neulich im Kindergarten: Tim und Lisa spielen ein Spiel. Sie nennen abwechselnd immer größere Zahlen. Wenn einem der beiden Kinder keine größere Zahl mehr einfällt, hat es verloren. Tim beginnt mit der Zahl 10. Lisa antwortet mit 20.
Tim kontert: 100. Lisa sagt: 101. So geht es eine ganze Weile weiter. Schließlich sagt Tim stolz: 1 Million. Dann hat Lisa eine Idee.
Sie sagt: „Ich nehme immer deine Zahl plus 1.“
Tim denkt einen Moment nach, dann sagt er siegesgewiss: „Meine nächste Zahl ist unendlich.“ Aber Lisa kontert erneut: „Dann ist meine nächste Zahl unendlich und 1.“
Doch wer hat denn jetzt gewonnen? Ist „unendlich“ eine Zahl? Wenn ja, ist dann „unendlich und 1“ auch eine Zahl und ist diese Zahl wirklich größer als „unendlich“?
Um diese Fragen beantworten zu können, müssen wir in die Mengenlehre eintauchen. Die Mengenlehre ist ein Spezialgebiet der mathematischen Logik, das am Ende des 19. Jahrhunderts von Georg Cantor begründet wurde.

Immer größere Zahlen, Teil 1: abzählbare Unendlichkeiten

Die natürlichen Zahlen, die man in der Schule kennenlernt, kann man einfach aufzählen, indem man immer „plus 1“ rechnet. Fängt man damit einmal an, dann sieht man bald, dass man nie fertig werden wird. Es gibt unendlich viele solche natürlichen Zahlen und, wie Lisa schon beobachtet hat, erhält man für jede natürliche Zahl eine nächste größere Zahl, wenn man „plus 1“ rechnet.
Man kann sich natürliche Zahlen auch als Mengen mit endlich vielen Elementen vorstellen. Eine Menge ist – vereinfacht ausgedrückt – wie ein Sack, in den man Dinge hineintun kann. Die Zahl 0 entspricht dann der leeren Menge, also einem Sack ohne Inhalt. Wir schreiben ∅ für die leere Menge.
Die Zahl 1 können wir darstellen als eine Menge, die ein Element enthält, und zwar die leere Menge. Dies schreiben wir als {∅}. Die Menge, die die Zahl 2 darstellt, hat nun zwei Elemente: die Zahlen 0 und 1. Formal schreiben wir diese Menge so: {∅,{∅}}. So kann man jede natürliche Zahl auf eine kanonische Art und Weise als Menge schreiben.
Warum stellen wir uns natürliche Zahlen als Mengen vor? Dieses Verständnis von Zahlen als Mengen hilft uns, unendlich große Zahlen besser zu verstehen. Wir schreiben ℕ für die Menge aller natürlichen Zahlen, unsere erste unendlich große Menge.
Nun können wir festlegen, was „unendlich plus 1“ sein soll: Wir definieren die nächstgrößere Zahl als die Menge ℕ∪{ℕ}. Dies ist die Menge der natürlichen Zahlen ℕ vereinigt mit der Menge {ℕ}, das heißt alle natürlichen Zahlen sind Elemente von dieser neuen Menge und die Menge der natürlichen Zahlen ist selbst ein Element. Damit hat die Menge ℕ∪{ℕ} ein Element mehr als die Menge ℕ und es macht Sinn, ℕ+1 für diese Menge zu schreiben.
Mit diesem Schema können wir immer größere Zahlen aufzählen und erhalten viele, verschieden große unendliche Mengen. Können wir eine Menge so bilden, handelt es sich um eine abzählbare Menge. In diesem Sinne kann Lisa also sagen, dass „unendlich plus 1“ tatsächlich größer als unendlich ist.

Immer größere Zahlen, Teil 2: überabzählbare Unendlichkeiten

Cantor hat gezeigt, dass es darüber hinaus unendlich große Mengen gibt, die man nicht mehr abzählen kann (Cantor, 1891).
Abzählen heißt hier, dass wir die Elemente einer gegebenen Menge mit Hilfe von natürlichen Zahlen durchnummerieren. Bei der Menge ℕ∪{ℕ} aus dem vorherigen Abschnitt ist dies zum Beispiel noch möglich, in dem man das Element ℕ mit 0 nummeriert und alle Elemente von 𝑛  mit der Zahl 𝑛+1 nummeriert.
Können wir die Elemente nicht so durchnummerieren, so ist die betreffende Menge überabzählbar. Ein berühmtes Beispiel für eine solche Menge ist die Menge der reellen Zahlen. Wir schauen uns in diesem Artikel aber die Menge aller Teilmengen der natürlichen Zahlen an.
Tim und Lisa ist mittlerweile ihr Spiel vom Anfang langweilig geworden. Tim schlägt daher ein neues Spiel vor: „Wir sortieren die Zahlen von 1 bis 100 in Gruppen ein. Wem keine neue Gruppe einfällt, verliert!“
Lisa beginnt: „Alle geraden Zahlen!“ Tim kontert: „Alle durch 9 teilbaren Zahlen."
Die beiden bilden Teilmengen der natürlichen Zahlen. Nehmen wir an, sie betrachten nicht die Zahlen bis 100, sondern alle natürlichen Zahlen. Könnten Lisa und Tim alle Teilmengen in ihrem Spiel nennen, selbst wenn sie unendlich viel Zeit haben?
Stellen wir uns zunächst vor, das wäre möglich und man könnte die Elemente dieser Menge abzählen. Jede solche Teilmenge kann man als Folge von Nullen und Einsen auffassen. Zum Beispiel zeigt das erste Element der Folge an, ob die Zahl „0“ ein Element der Menge ist. Das zweite Element zeigt an, ob die Zahl „1“ ein Element der Menge ist, und so weiter.
Hierbei bedeutet 0, dass die jeweilige Zahl kein Element der Menge ist, und 1 bedeutet, dass sie Element der Menge ist. Am Beispiel wird klarer, was hier gemeint ist.
Nehmen wir eine Menge, die die Zahlen 1, 5, 6 und 7 enthält. Diese können wir wie folgt als Folge von Nullen und Einsen auffassen:

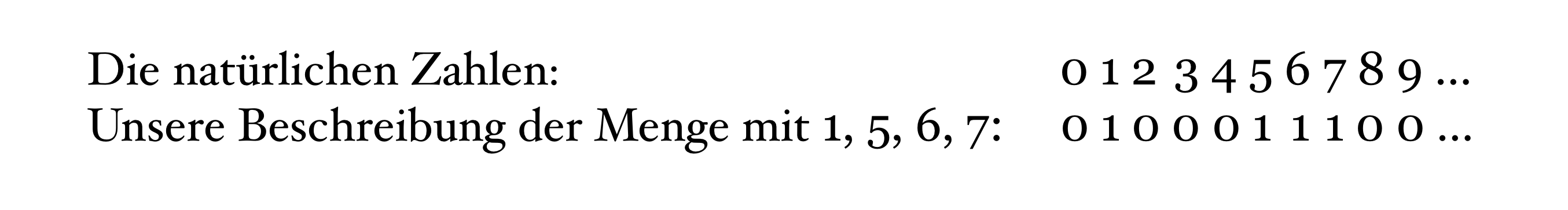
Das funktioniert auch für unendliche Mengen. Für die Menge der geraden Zahlen sieht die zugehörige Folge von Nullen und Einsen zum Beispiel so aus:

Nun können wir alle Teilmengen der natürlichen Zahlen mit Hilfe von diesen Auffassungen als Folgen von Nullen und Einsen in einer (unendlich langen) Liste untereinanderschreiben (wir haben ja angenommen, dass wir sie abzählen können). Unsere Liste könnte zum Beispiel wie folgt anfangen:

Schauen wir uns einmal die rot markierte Folge auf der Diagonalen an: 0 0 0 1 0 1 1 0 …
Wenn wir jede 1 durch eine 0 ersetzen und andersherum, ergibt das wieder eine Folge von Nullen und Einsen (und damit eine Teilmenge der natürlichen Zahlen). Dann fängt die Folge so an: 1 1 1 0 1 0 0 1 ….
Dadurch, dass wir die erste Null durch eine Eins ersetzt haben, ist unsere neue Folge sicher von der ersten Folge auf unserer Liste verschieden. Genauer gesagt haben wir sichergestellt, dass sich unsere neue, diagonale Folge von jeder horizontalen Folge auf der Liste unterscheidet, da wir auf der Diagonalen jede Eins durch eine Null ersetzt haben oder andersherum.
Da die neue Folge auch eine Folge von Nullen und Einsen ist, muss sie irgendwo in unserer Liste auftauchen. Doch genau das kann nicht sein, da sie sich von allen anderen Folgen mindestens durch eine Stelle unterscheidet.
Wir erhalten also einen Widerspruch: Wir hatten angenommen, dass wir alle Folgen von Nullen und Einsen in einer Liste untereinander aufschreiben können. Nun haben wir aber eine Folge von Nullen und Einsen gefunden, die nicht in unserer Liste auftaucht. Damit kann es also keine Liste geben, die alle Folgen von Nullen und Einsen erfasst.
Mit anderen Worten: Unsere Annahme, dass wir alle Folgen von Nullen und Einsen (bzw. alle Teilmengen der natürlichen Zahlen) in einer Liste aufschreiben können, muss falsch sein: Tim und Lisa können, selbst wenn sie unendlich lange spielen, keinen Verlierer feststellen.
Mengen mit dieser Eigenschaft heißen überabzählbar (Deiser, 2021). Sie sind auf eine Art unendlich, dass man ihre Elemente nicht mehr abzählen kann. In diesem Sinne sind sie eine größere Unendlichkeit, als etwa die abzählbar unendlichen natürlichen Zahlen. So erhalten wir eine Hierarchie von immer größer werdenden Unendlichkeiten.

Zahlen, deren Existenz man nicht beweisen kann

Wir haben bisher gesehen, dass Zahlen als Mengen verstanden werden können und dass selbst unendliche Mengen unterschiedlich groß sein können. Doch gibt es noch größere Mengen beziehungsweise Zahlen? Dieser Frage geht die zeitgenössische Forschung der Mengenlehre nach: Hier betrachten wir sogar Zahlen, die so groß sind, dass wir nicht einmal beweisen können, dass diese Zahlen existieren. Was heißt das genau?
Mit dem Diagonalverfahren von Cantor, das wir uns im vorigen Abschnitt angeschaut haben, können wir immer größere Unendlichkeiten konstruieren. Wir nennen solche Unendlichkeiten, die die Größe von Mengen beschreiben, Kardinalzahlen.
Anstatt einfach immer größere Kardinalzahlen zu konstruieren, fragen wir uns nun, ob es Kardinalzahlen (oder auch einfach unendlich große Mengen) mit bestimmten „schönen und nützlichen“ Eigenschaften gibt.
Diese schönen Eigenschaften sollen sicherstellen, dass die Kardinalzahlen besonders große unendliche Mengen sind, daher nennen wir sie große Kardinalzahlen. Genauer gesagt sind diese großen Kardinalzahlen sogar Axiome, das heißt Anforderung, die wir an unser mathematisches Universum stellen können, aber von denen wir nicht mit den Standardmethoden zeigen können, dass sie wahr sind. Ein Beispiel für ein solches Großes- Kardinalzahl-Axiom ist die Existenz von unerreichbaren Kardinalzahlen.
Diese Zahlen sind so groß, dass sie nicht durch einfache Methoden mit kleineren Zahlen angenähert werden können. Das heißt, sie sind zum Beispiel keine Nachfolger von anderen Zahlen, so wie zum Beispiel 2 ein Nachfolger von 1 ist.
Außerdem kann man sie nicht als Grenzwert von kleineren Zahlen bekommen, zumindest wenn man den Grenzwert von Zahlen nimmt, deren Anzahl eine kleinere Unendlichkeit ist als die Zahl, die wir erreichen wollen.
Zudem entsteht eine unerreichbare Kardinalzahl beispielsweise auch nicht als Menge aller Teilmengen einer kleineren Zahl. Die Menge der natürlichen Zahlen hat diese Eigenschaften von Unerreichbarkeit, da Nachfolger von endlichen Zahlen und auch Mengen von Teilmengen von endlichen Mengen wieder endlich sind.
Das heißt, mit Hilfe von endlich vielen natürlichen Zahlen kann man niemals die Menge der gesamten natürlichen Zahlen erreichen, zumindest nicht in endlich vielen Schritten. Die Existenz von größeren Unendlichkeiten mit diesen Eigenschaften kann mit den klassischen Methoden der Mathematik nicht bewiesen werden, hat aber zahlreiche sehr interessante Konsequenzen. In der Mengenlehre betrachten wir sogar noch größere Zahlen, zum Beispiel sogenannte messbare Kardinalzahlen, Woodin Kardinalzahlen und superkompakte Kardinalzahlen. Eine Möglichkeit, die sehr großen Kardinalzahlen besser zu verstehen, bietet die Betrachtung von unendlichen Spielen.

Unendliche Spiele

Eine Anwendung von großen Kardinalzahlen findet sich in der Analyse von unendlich langen Spielen. Dazu betrachten wir Spiele mit zwei Spielern, wie Tim und Lisa aus dem Kindergarten. Der interessante Punkt ist, dass diese Spiele unendlich lange dauern – genauer gesagt: so lange wie es natürliche Zahlen gibt. Der Einfachheit halber betrachten wir nur Spiele, in denen die beiden Spieler im Wechsel natürliche Zahlen spielen, so wie im Spiel von Tim und Lisa. Dann sieht ein Spielverlauf zum Beispiel wie folgt aus:

Je nachdem, welche Eigenschaft die Folge der natürlichen Zahlen hat, die im Spielverlauf produziert wird, entscheiden wir, ob Tim oder Lisa gewinnt. Der Sieger steht im Normalfall erst nach unendlich vielen Schritten fest. Da wir so lange nicht warten wollen, ist es hilfreich zu verstehen, ob Tim oder Lisa eine Gewinnstrategie haben. Dann müsste man nicht bis zum Ende des Spiels warten, um zu sehen, wer gewinnen wird (wenn wir davon ausgehen, dass die beiden einer Gewinnstrategie folgen würden und zum Beispiel keine Flüchtigkeitsfehler machen).
Eine Gewinnstrategie (sagen wir für Tim) ist eine Vorschrift, die Tim seine Spielzüge vorgibt (abhängig von Lisas Spielzügen), sodass Tim, wenn er sich an diese Vorschrift hält, auf jeden Fall gewinnt. Genauso können wir Gewinnstrategien für Lisa definieren.
In unserem Beispiel vom Anfang ist Lisas Einfall: „Ich nehme immer deine Zahl plus 1“, eine Gewinnstrategie für Lisa (selbst wenn wir Tim und Lisa erlauben, unendlich große Zahlen zu spielen). Im Allgemeinen und für kompliziertere Spiele ist nicht klar, ob es immer eine solche Gewinnstrategie für Tim oder Lisa gibt.
Was hat dies nun mit sehr großen Unendlichkeiten und großen Kardinalzahlen zu tun?
Historisch gesehen zunächst nicht viel, beide Gebiete sind unabhängig voneinander seit Mitte des 20. Jahrhunderts entstanden. Doch in den 1970er und 1980er Jahren gab es eine Revolution in der Forschung an großen Kardinalzahlen und Gewinnstrategien für unendliche Spiele: Es konnte gezeigt werden, dass die Existenz von sehr großen Kardinalzahlen impliziert, dass es in bestimmten unendlich langen Spielen immer für einen der beiden Spieler eine Gewinnstrategie gibt (Martin, 1970) (Martin, Steel, 1989) (Neeman, 2002).
Dieser Zusammenhang ist nicht nur überraschend, sondern auch sehr komplex. Die resultierenden Gewinnstrategien sind zum Beispiel nicht konstruktiv, das heißt es ist nicht bekannt, wie diese aussehen. Dennoch kann man beweisen, dass diese Gewinnstrategien existieren, wenn sehr große Kardinalzahlen existieren.
Anstatt eine Gewinnstrategie konkret zu konstruieren, beweist man vielmehr, dass es nicht sein kann, dass keiner der beiden Spieler eine Gewinnstrategie hat. Nun könnte es natürlich der Fall sein, dass die großen Kardinalzahlen für diese Resultate gar nicht nötig sind. Vielleicht kann man ja auch „einfach so“ beweisen, dass in diesen Spielen immer einer der beiden Spieler eine Gewinnstrategie hat.
Doch dem ist nicht so: Interessanterweise ist der Zusammenhang zwischen sehr großen Kardinalzahlen (genauer gesagt: kleinen kanonischen Modellen mit sehr großen Kardinalzahlen) und Gewinnstrategien in bestimmten unendlich langen Spielen sogar eine Äquivalenz (Harrington, 1978) (Müller, et al., 2020). Das heißt die Existenz von sehr großen Kardinalzahlen impliziert die Existenz von Gewinnstrategien und gleichzeitig impliziert die Existenz von Gewinnstrategien auch die Existenz von sehr großen Kardinalzahlen (genauer und mathematisch korrekt gesagt: die Existenz von kleinen kanonischen Modellen mit sehr großen Kardinalzahlen).
Diesen unerwarteten, aber sehr tiefgreifenden Zusammenhang besser zu verstehen, ist eines der Hauptprobleme aktueller Forschung in der Mengenlehre und motiviert mich tagtäglich, die komplexen Fragestellungen dieses Forschungsgebietes anzugehen und zu lösen.
Zusammenfassend kann man an dieser Stelle festhalten, dass die Frage, was nach unendlich kommt, keine einfache abschließende Antwort besitzt. Die klassischen Methoden der Mathematik liefern keine Antwort auf diese Frage. Die Mengenlehre bietet jedoch einen bunten Strauß verschiedenster, unterschiedlich großer Unendlichkeiten mit sehr vielen Möglichkeiten, diese in verschiedenen Fragestellungen auch anzuwenden.